Unity in a Kaleidoscope: A Geometric Artwork
- Lucy Carter

- May 30, 2023
- 3 min read
Updated: Dec 31, 2023
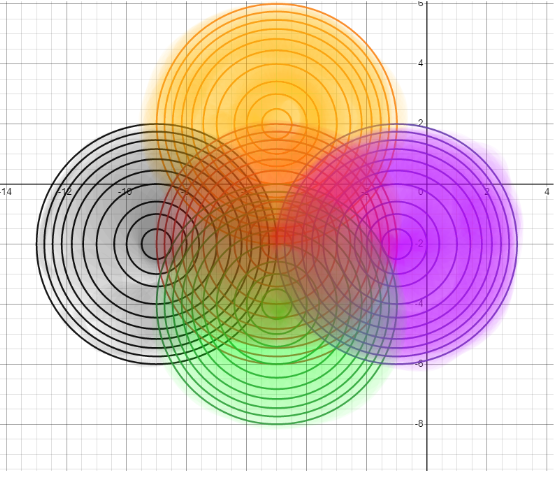
Note: This is just an extra school project I did a couple weeks ago for math class; it is essentially a small art project that incorporates basic coordinate geometry into "circle art." This is an art project I made with a digital graph and painter. It's not super advanced or artistic, but below provides the thought process behind this project; note that this essay was formatted for the original school assignment. :)
Unity in a Kaleidoscope is a geometric artwork consisting of five differently colored circles with the exact same pattern: a series of ten “rings” that share the same center and contain gradually decreasing radii as the eye moves further to the center.
Although these circles contain different centers and locations, they are all congruent. Each one would simply need to be translated a certain amount of units to map another. For instance, the orange pattern would simply need to be translated four units to the left and four units down in order to map the black pattern. Likewise, the black pattern would simply need to be translated eight units to the right in order to map the purple pattern.
Because each of these circles each contain ten “rings,” each color is represented by ten equations.
The outer edge of the orange pattern, for instance, can be represented by the equation (x+5)^2 + (y-2)^2=16. This means that the circle has a center of (-5,2), and a radius of sqrt (16), or 4.
Likewise, the outer edge of the black circle can be represented by the equation (x+9)^2 + (y+2)^2=16, the outer edge of the red circle can be represented by the equation (x+5)^2 + (y+2)^2=16, the outer edge of the green circle can be represented by the equation (x+5)^2 + (y+4)^2=16, and the outer edge of the purple circle can be represented by the equation (x+1)^2 + (y+2)^2=16. As seen here, each of the circles have the same radius, even though they have differing centers: (-5, 2), (-9, -2), (-5, -2), (-5, -4), and (-1,-2), respectively.
The rest of the nine circles inside each pattern have radii of sqrt (14), sqrt (12), sqrt (10), sqrt (8), sqrt (6), sqrt (4), sqrt (2), sqrt (1), and sqrt (0.25). (In other words, each consecutive radicand decreases by two until it reaches sqrt (0.25), or 0.5.) As mentioned previously, all circles in each color share the same center, so r in the equation (x-h)^2 + (y-k)^2 = r^2 would equal the radicand of one of the values mentioned previously and the values of h and k would be replaced with the coordinates of the centers. For instance, the smallest ring in the black circle has an equation of (x+9)^2 + (y+2)^2 = 0.25.
The congruence of each corresponding circle—their shared radii and their abilities to map map one another with some simple translations—establishes the unity in the artwork Unity in a Kaleidoscope. Although a total of fifty different equations were used to create this composition, these fifty equations ultimately generated a structured, geometric pattern shared by all five colors. The 50 equations ultimately established simplicity and structure within my composition.
However, the overlap in the center and the variation in color amplifies this composition, adding more depth and complexity to such a simple, geometrically structured image. Had each shape been pigmented with a solid black and translated away from one another, this composition would have merely been four patterns, not a colorful, more kaleidoscopic pattern. The overlap of each color and pattern creates new mixtures of color and shapes, thereby inspiring me to call this composition Unity in a KALEIDOSCOPE, not just Unity.




Comments