Three Pros (and Three Cons) of Common Core Math Methods

Written by a student who has been taught with Common Core Standards

Have you been taught long division or partial quotients? Do you add and subtract numbers arithmetically, or do you use a number line to do so?

In other words, have you been taught mathematics traditionally or taught mathematics with Common Core standards?

Common Core Standards are a series of relatively recent educational standards that detail the milestones students from kindergarten to twelfth grade should reach by the end of each year of schooling. Each grade level is set with certain standards in English Language Arts and, of course, mathematics.

Due to the recency of Common Core standards, parents may find themselves puzzling over a seemingly simple fourth grade homework question in their child's math paper; these standards have not been initiated until 2010, so many parents may not even know what these standards are and what it is like to be taught with them.

This may bring parents and teachers to wonder: Are these standards effective? What is it like to be educated with these standards? What do students actually think about these standards? As a student who has been educated with Common Core math standards myself, I would like to provide a first-hand account of my experiences with common core.

Disclaimer: Please note that I am not a scholar or educator. This article is merely an opinion piece that is representative of my opinions. Other students my age may feel differently about Common Core math strategies, and teachers may or may not agree with the content of this article. Additionally, this is not an exhaustive list of all Common Core strategies; this article should not replace a comprehensive mathematical education. I highly recommend visitng the Common Core website to learn these standards.

Three Pros (and Three Cons) of Common Core Math Strategies!

PRO: Number Sense and Numerical Reasoning

Number sense, as implied by the name, is the ability to make sense of numbers and the quantities they represent in order to perform certain operations. If taught and introduced correctly, common core math strategies can better establish numerical reasoning and enable students to better grasp and manipulate certain quantities.

Take different approaches to division, for instance. Traditionally, we may approach a math problem with the textbook long division method: calculate how many times the divisor can go into part of the dividend, write this factor as part of the quotient according to its place value, subtract the product of the divisor and the factor from the dividend, and proceed on until you reach a remainder, a repeating decimal, or until you have no remaining numbers. While the long division method can still teach number sense and numerical reasoning if a teacher explains the "logic" behind why it works, this method can still be quite formulaic---it is easy for a student to blindly copy down the steps and carry on with the procedures without understanding what is actually happening and how the quotient comes to be.

However, a different approach, called partial quotients, can fix this. Unlike long division, which requires you to calculate the maximum number of times the divisor can go into the dividend with little room for error, partial quotients is a bit more flexible and can be a bit less textbook-oriented and more focused on grasping actual quantities. Let's take the problem 471/35. One may argue, with long division, that 35 goes into 47 once and then incorporate this into the quotient and proceed on with division from there. However, with partial quotients, one may easily calculate that 35*10=350 and then subtract that from 471 and put 10 next to your problem. 471-350=121. You can continue on as follows:

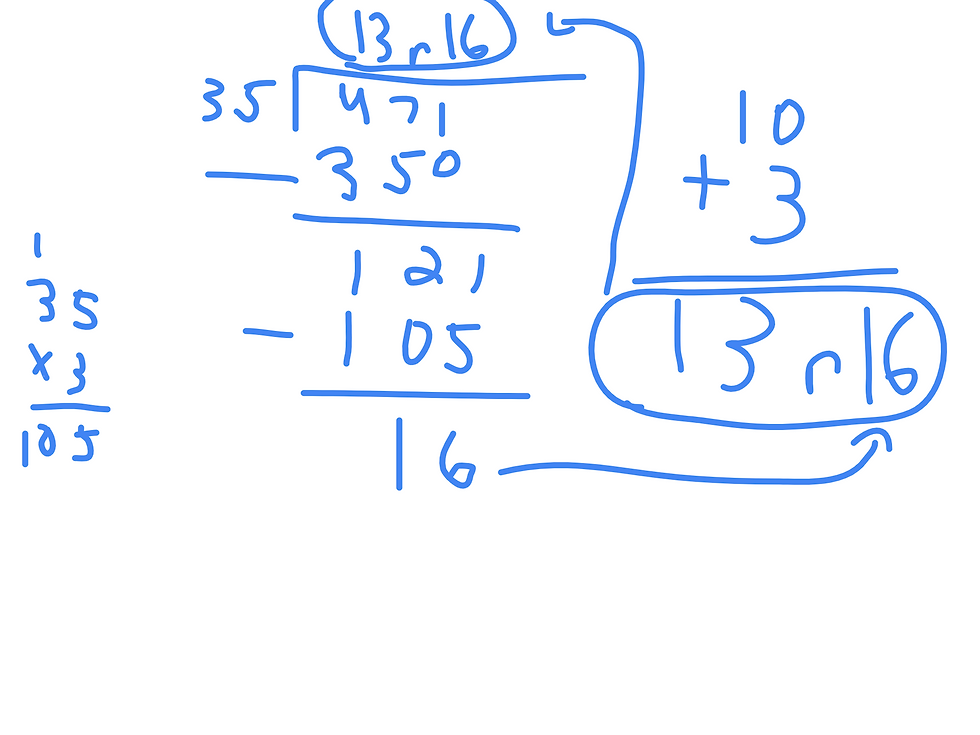
As seen here, partial quotients more directly illustrates the place value and number sense that could more easily be overlooked in long division. Students can reason that because 35 can go into 471 ten and three times, it makes sense to add these two numbers to find the quotient---13, with a remainder of 16. I would argue that it is much easier to make sense of the quantities you are manipulating using partial quotients than using long division.

CON: Inefficiency

While Common Core methods like partial quotients can help students better understand the processes and quantities that go into division, they can be quite inefficient. Referring back to partial quotients, there can be a lot of inefficiency associated with it due to its trial-and-error approach. In addition to having to calculate how many times the divisor goes into the dividend and follow the usual process of subtraction, there is also having to test and calculate different numbers that could be multiplied by the divisor, as well as having to add all the factors together to calculate the quotient. Work can be very inefficient and messy, especially when making calculations with large quantities with number facts you may not be able to remember or calculate at the top of your head. Long division definitely could have saved you all of those steps.

Compare partial quotients:

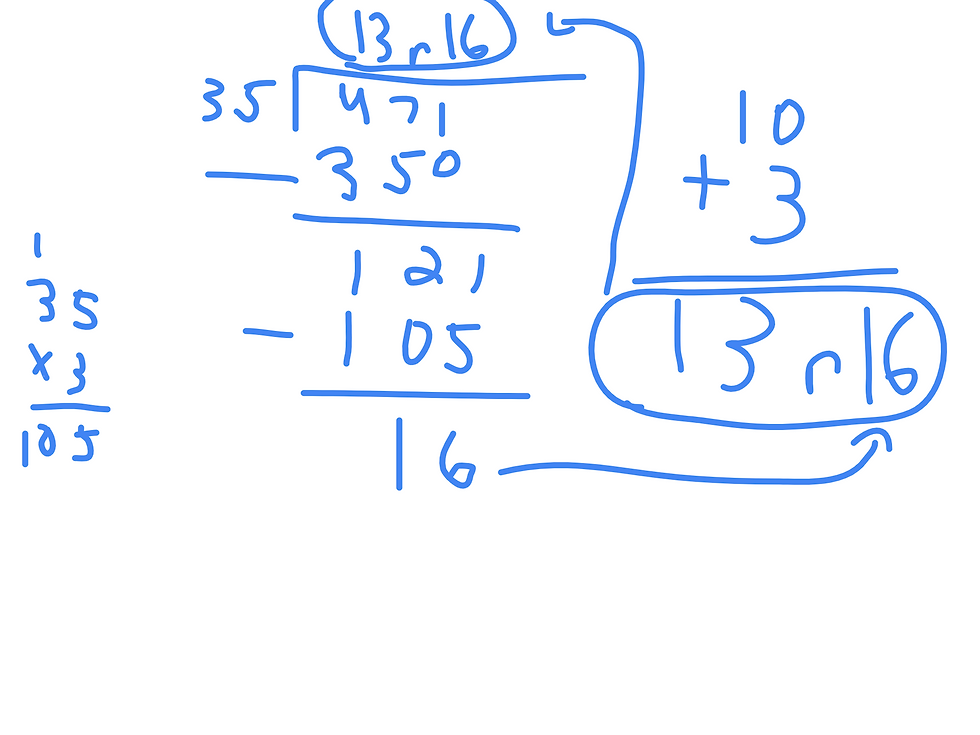
to the fewer steps of long division:

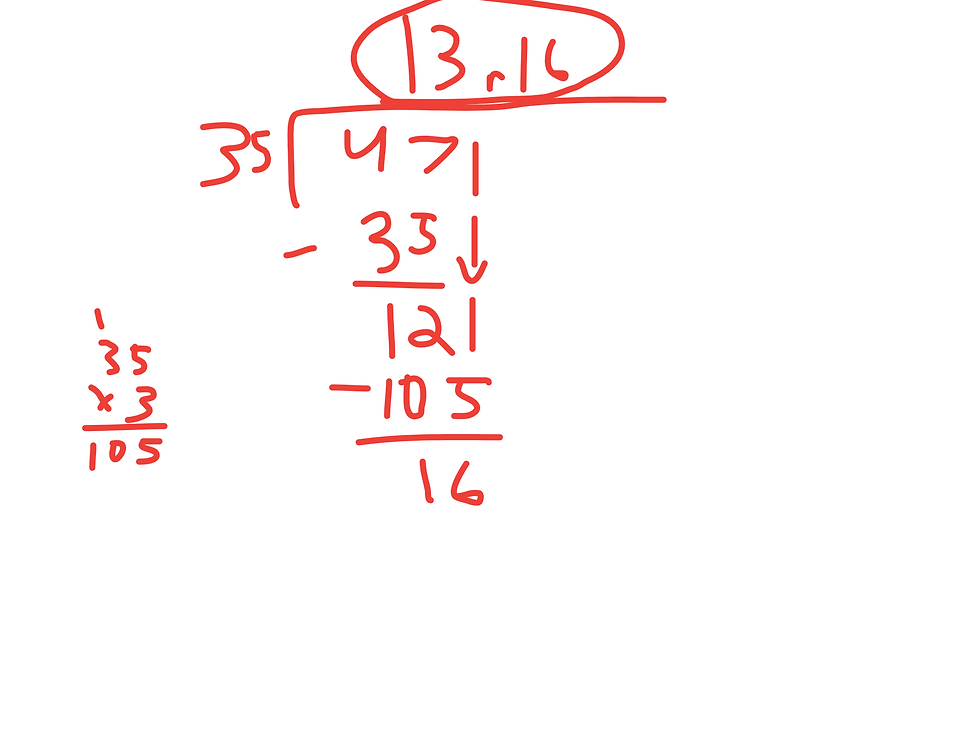
There is no extra adding and little trial and error; you can quickly and more directly get to your answer with long division!

PRO: Lateral thinking

If there is one thing Common Core is good at, it's helping students think creatively and outside the box. Take the multiplication problem 3*5. Traditionally, students may derive the answer simply by memorizing math facts: 3*5=15 (duh). Common core, meanwhile, can actually help students illustrate this situation visually and creatively with the area model. We can draw a rectangular model with three columns and five rows (or vice versa) to visually model how and why 3*5=15:

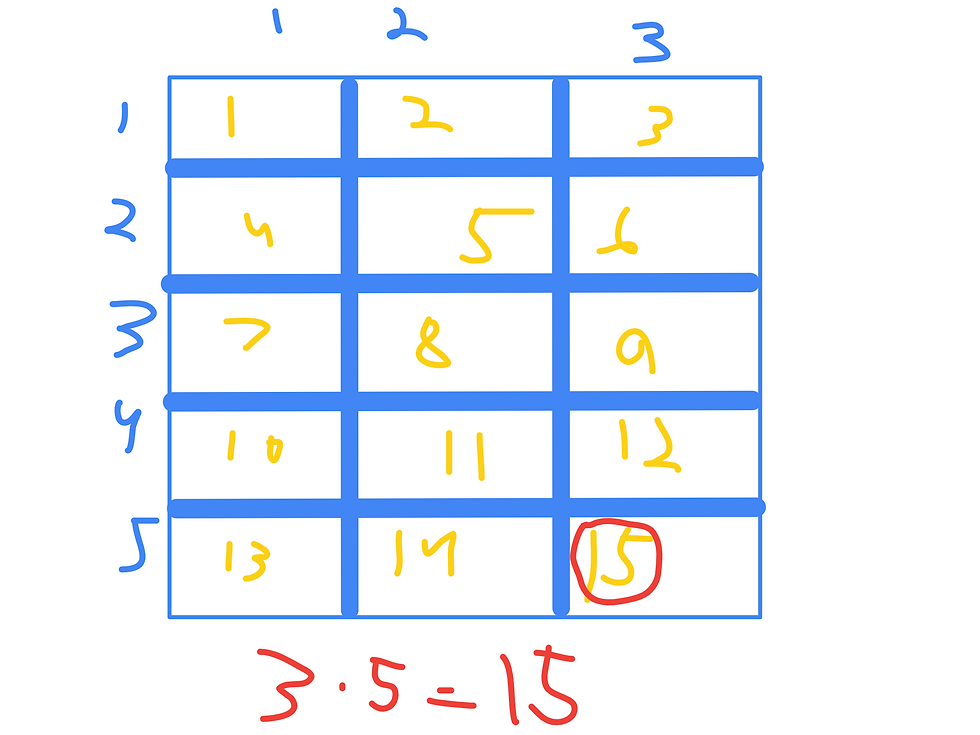
The area model allows students to understand that with 3*5, there are three groups (columns) of five (rows), which therefore add together to get 15. Similarly, students can reason that there are five groups of three and get the answer from there.

Likewise, you can use the area model to break down multi-digit numbers into smaller pieces and calculate the product via additon:

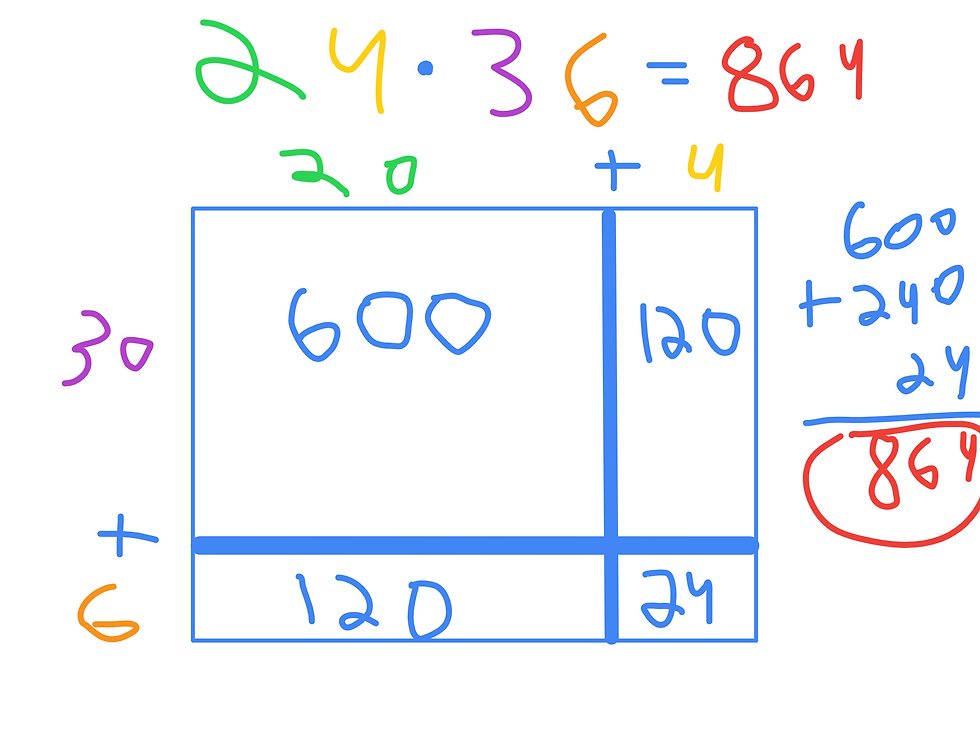
This method helps students to think laterally and creatively when it comes to multiplication---it teaches students to break larger tasks into smaller components and visualize the abstraction of arithmetic with basic geometry: the area of a square/rectangle!

CON: Overthinking

That said, I do have to admit that while Common Core strategies like the area model do enable lateral thinking, they also can lead to overthinking.

Do you really need to draw an entire area model just to solve a problem as simple as 3*5? It is such a simple math fact to memorize; why overcomplicate it with an area model? Similarly, while the area model can help students break down large tasks into smaller bits with multi-digit multiplication, I do not see why it is wrong to just solve the problem arithmetically the traditional method. So long as you are able to understand place value and reason through the problem, I really do not see why it is so wrong to solve a math problem with simpler methods like traditional multiplication, mental math, or the memorization of math facts.

PRO: Mathematical Modelling

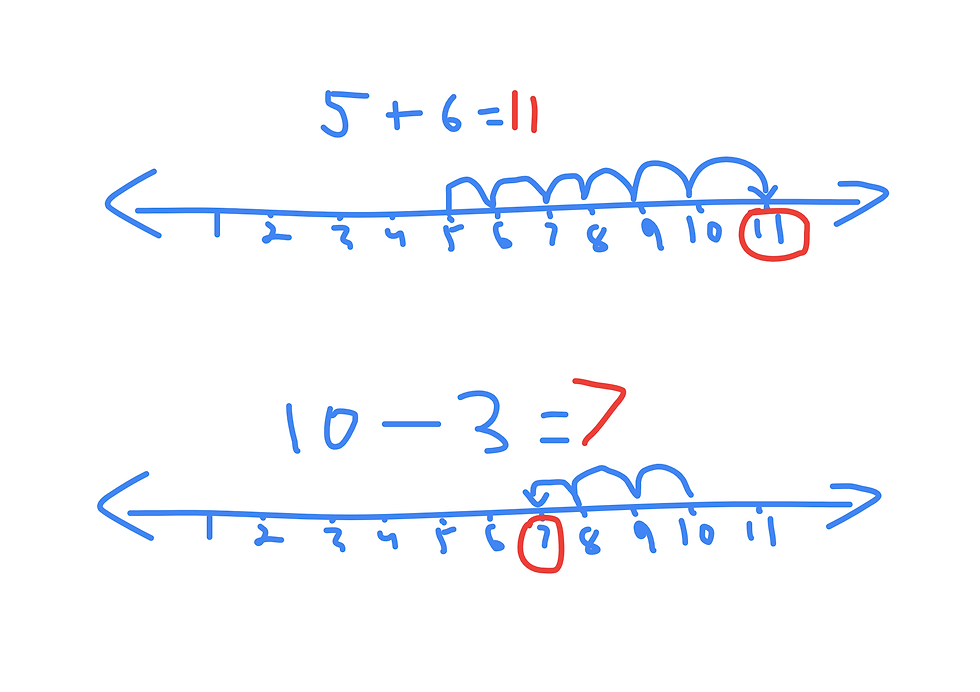
The above image is a strategy taught early when I was in elementary school that uses the number line to visualize addition and subtraction.

Indeed, common core approaches to mathematics can be very beneficial when it comes to modelling mathematical operations. For instance, we can model the act of adding six to five by starting at five and "jumping" forward six times in order to calculate the sum: 11. Similarly, we can model the act of subtracting three from 10 by starting at ten and "jumping" back three times to calculate the difference. Strategies like the number line can definitely make arithmetic operations more tangible than they would have been if tradtionally taught.

CON: Extra busywork

Probably one of the largest cons from the perspective of the seven to nine year olds being taught common core is the extra busywork. A simple problem like 10-3 could have been solved in seconds with mental math or memorizing math facts, but with the emergence of common core standads, you may now have to draw or annotate an entire number line just to get credit for a single problem. While number sense, mathematical modelling, and creative and lateral thinking can arise from common core standards, teachers and parents should also look at things from a student's perspective: my dear teachers, do you think children aged 7-11 years would care to appreciate mathematical modelling and number sense when it comes at the cost of drawing extra models and doing extra work in the long-run? I certainly appreciate the nuances of mathematical modelling now, but how could you expect eleven-year-old me to feel the same?

Common core is the object of debate. There are a variety of pros as well as a variety of cons associated with common core math strategies. Numerical reasoning, lateral thinking, and mathematical modelling are three excellent benefits that can be reaped from Common Core approaches to mathematics. Meanwhile, common core can still lead to inefficient methods, overthinking, and extra busywork. What do you think?

Do you think Common Core math does more good or more harm to students?

• Good!
• Harm!